E’ possibile osservare in Natura la trasformazione di energia in materia? Dalla luce alla materia: ora è possibile.
E’ possibile osservare in Natura la trasformazione di energia in materia? Dalla luce alla materia: ora è possibile.
Segnalato dal Dott. Giuseppe Cotellessa

E=m⋅c2
E0=m0⋅c2
E=m0⋅c2+12m0⋅v2=m0⋅c2(1+12v2c2)
E=m0c21–v2c2−−−−√=m0 ⋅c2 γ
k=m0⋅c2 γ –m0⋅c2=m0⋅c2( γ–1)
m= m0⋅γ
p=mv=m0⋅γ⋅v=m0⋅v1–v2c2−−−−√
E=mc2
E=mc21−v2c2−−−−−√
β=vc
E=m1−β2−−−−−√
E2=m2+p2

 a.L'acceleratore Hera del laboratorio Desy di Amburgo: un anello con una circonferenza di 6,3 km capace di far collidere protoni con elettroni per esplorare la struttura dei protoni fino a scale di dimensioni di 10-15 mm (un milionesimo di miliardesimo di mm).
a.L'acceleratore Hera del laboratorio Desy di Amburgo: un anello con una circonferenza di 6,3 km capace di far collidere protoni con elettroni per esplorare la struttura dei protoni fino a scale di dimensioni di 10-15 mm (un milionesimo di miliardesimo di mm).
Luce virtuale
Fotoni contro fotoni

Segnalato dal Dott. Giuseppe Cotellessa

Equivalenza massa-energia
La fisica classica prevede che l’energia possa essere espressa in varie forme (cinetica, potenziale, …), ma che in generale essa si conserva; anche la massa di un sistema si conserva in seguito ad un certo fenomeno fisico per la legge di Lavoisier; tale legge prevede, infatti, che in una qualsiasi reazione chimica la massa dei reagenti deve essere uguale a quella dei prodotti.
Nella teoria della relatività, però, anche queste affermazioni perdono validità; Albert Einstein, infatti, affermò che la massa e l’energia sono quantità fisiche collegate tra loro, e in particolare il rapporto che c’è tra esse dipende dal quadrato della velocità della luce nel vuoto.
Questa relazione si traduce nella famosa formula:
dove E indica l’energia complessiva del corpo in questione (espressa in J), cioè la somma di tutte le energie che esso possiede; m indica la massa del corpo a riposo (espressa in kg); c è la velocità della luce nel vuoto (espressa in m/s).
Da questa relazione si può dedurre che la massa di un corpo non si conserva come prevedeva la fisica classica, ma varia in base alle variazioni di energia cui il corpo è sottoposto.
Di conseguenza, se il corpo assorbe energia si avrà un aumento della sua massa; se esso cede energia, invece, anche la massa subisce una diminuzione.
La massa di un corpo, quindi, è in ogni caso una forma di energia; qualsiasi corpo, quindi, che ha massa possiede una quantità di energia pari a mc2 .
Energia di un corpo a riposo
Si definisce l’energia di un corpo a riposo come il prodotto del quadrato della velocità per la massa a riposo del corpo:
In generale un corpo in movimento, possiede energia cinetica; quindi, l’energia totale del corpo sarà data dalla somma di tutte le energie che esso possiede:
L’espressione tra parentesi può essere approssimata, ( nel caso in cui la velocità v è molto piccola rispetto a c), come coefficiente di dilatazione γ; l’equazione generale dell’energia, quindi, assume la seguente forma:
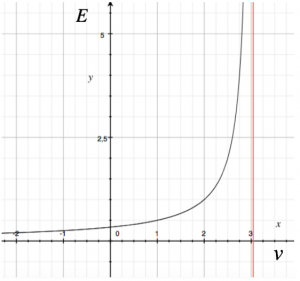
Rappresentando il grafico dell’energia E in funzione della velocità v, notiamo che la curva presenta un asintoto verticale v = c;

possiamo dedurre, quindi, che se la velocità del corpo si avvicina a quella della luce, la sua energia aumenta, fino a raggiungere un valore infinito.
Ciò significa che un corpo si può muovere alla velocità della luce solo se esso possiede una quantità infinita di energia; dato che ciò non è possibile nella realtà, otteniamo un’ulteriore conferma del fatto che velocità della luce non può essere raggiunta da nessun corpo che possiede massa, e rappresenta quindi una velocità limite.
L’energia cinetica relativistica
Conoscendo l’espressione generale dell’energia totale di un corpo, possiamo definire l’energia cinetica relativistica; essa corrisponde alla differenza tra l’energia totale e l’energia che il corpo possiede quando è fermo, cioè l’energia a riposo del corpo.
L’energia cinetica, quindi, assume la seguente espressione:
A partire dall’energia totale, inoltre, possiamo anche definire la massa relativistica di un corpo; essa è data dal prodotto della massa a riposo del corpo per il coefficiente γ:
Vediamo, quindi, che con il variare della velocità del corpo, non solo si modificano tempi e lunghezze, ma anche la massa subisce variazioni. Mano a mano che la velocità diminuisce, la massa del corpo diventa sempre più piccola; per v=0 si raggiunge il valore minimo, corrispondente a quello della massa a riposo.
Come sappiamo, per un corpo che ha massa e si muove a velocità v, possiamo definire la quantità di moto del corpo come prodotto della massa per la velocità. Avendo introdotto il concetto di massa relativistica, è naturale parlare anche di quantità di moto relativistica, che si esprime come:
La si trova dappertutto, simbolo dei trionfi (e anche dei disastri, se pensate all'energia nucleare) della fisica moderna del 900.Cosa dice questa formula? Ci rivela la geniale scoperta di Einstein: un corpo di massa m a riposo è un incredibile serbatoio di energia E , che può essere calcolata come il prodotto della sua massa m per il quadrato della velocità della luce c .
Quello che è un peccato è che la formula più famosa del mondo - così come è scritta lassù - ha almeno due difetti. Primo, vale solo per corpi a riposo: appena ci si sposta in un sistema di riferimento in cui il corpo in questione si muove, beh, non vale più (tra un minuto vediamo perché questo è un bel limite alla comprensione); la formula generale, quella che vale per un corpo qualunque sia la sua velocità v , è questa:
Secondo, usa delle unità di misura innaturali, che aggiungono una complicazione probabilmente inutile alla formula, e, di nuovo, alla comprensione.
Iniziamo dalle unità di misura. La relatività speciale di Einstein ci dice che nulla si può muovere a una velocità maggiore di quella della luce c . A pensarci bene, se esiste una velocità limite, allora sarebbe sensato misurare ogni velocità in termini di questa velocità massima. Avrebbe molto più senso (perlomeno quando si fa fisica, forse non in autostrada) dire che un corpo viaggia a un centesimo della velocità della luce, piuttosto che a 3000 chilometri al secondo. Se decidiamo di usare questa convenzione (come tutti i fisici delle particelle fanno), possiamo ribattezzare la velocità come:
Se un corpo viaggia alla velocità della luce, avrà β=1 . Se va a 3000 chilometri al secondo, avrà β=0.01 . E naturalmente misurare le velocità in unità di c equivale a dire che c=1 , per cui la nostra formula iniziale (quella che vale per tutte le velocità) diventa:
Un po' più semplice, no? Siccome β non ha dimensioni (nel senso che è un numero puro, senza unità di misura), il trucchetto ci permette di misurare le masse e le energie (e i momenti, come vedremo tra un attimo) nella stessa unità di misura (scegliete voi quelle che vi piacciono: ai fisici delle particelle piacciono gli elettronvolt). Adesso facciamo un po' di magia con l'algebra (ce la potete fare!). In relatività il momento di un corpo si calcola come p=Eβ , per cui se manipolate un po' l'ultima formuletta (fate il quadrato, moltiplicate a destra e sinistra per 1−β2 , ...) potete ottenere questa qui:
che, detto tra noi, dovrebbe prendere il posto di formula più famosa del mondo!
Eh si, possiamo scrivere la formula più importante della relatività ristretta come fosse il teorema di Pitagora. Il quadrato dell'energia di un corpo è uguale alla somma dei quadrati della sua massa e del suo momento.
Guardate questa figura:

Nel caso (1) il corpo è fermo: la sua energia è completamente determinata dalla sua massa. Se il corpo in questione si muove ha un momento molto più piccolo della sua massa (2), e la sua energia è ancora quasi completamente determinata dalla sua massa solamente. E' il caso dei movimenti di tutti i giorni, della fisica classica: piccole velocità e grandi masse. Ma se il momento della particella è molto più grande della sua massa (2) come nel caso delle particelle negli acceleratori che viaggiano a velocità prossime a quelle della luce, beh, l'energia della particella è praticamente tutta determinata dalla sua velocità! E nel caso estremo di particelle senza massa (4) come il fotone, beh, queste viaggiano sempre... alla velocità della luce.
Adesso provate a usare questa figura per capire che cosa succede in un acceleratore di particelle. Prendete due particelle leggerine (diciamo sue protoni, come in LHC) e acceleratele a velocità prossime a quella della luce: siete nella condizione (3). Poi le fare sbattere l'una contro l'altra, e, come già sapete, avete a disposizione nello scontro la somma delle energie. Ovvero un'ipotenusa blu bella lunga. Adesso immaginate che nello scontro saltiate dalla condizione (3) a quella (2) (o anche (1), se volete): con l'energia a disposizione potete produrre particelle moooolto più pesanti (con un cateto verde molto più lungo), ma che si muovono decisamente più piano (un cateto rosso più corto). Questo è quello che fanno i collisionatori: trasformano energia cinetica (che è facile accumulare, accelerando particelle leggere) in massa. Producendo particelle più pesanti di quelle di partenza! E, naturalmente, potreste farlo anche saltando da (4) a (2), usando due fotoni energetici per produrre particelle massive.
Oliver Pike è un fisico del Blackett Laboratory presso l’Imperial College di Londra, Regno Unito, e insieme ad alcuni suoi colleghi si è messo in testa di ottenere la materia utilizzando solamente fasci di luce. In un suo studio pubblicato su Nature Photonics, Pike spiega di avere trovato il modo di farlo e risolvere così una delle più grandi e affascinanti sfide della fisica moderna, su cui si sono scervellati per decenni molti ricercatori in giro per il mondo. La ricerca spiega come si può fare per ottenere la materia dalla luce: manca ancora il passaggio alla pratica, che secondo i fisici del Blackett Laboratory sarà effettuato entro i prossimi 12 mesi.
Steven Rose, uno dei ricercatori che ha firmato lo studio, ha detto al Guardian di avere “dimostrato in linea di principio che si può ottenere la materia dalla luce: facendo l’esperimento sarà possibile provarlo”. L’obiettivo del gruppo di fisici per ora non è naturalmente trarre dalla luce qualcosa di visibile a occhio nudo: l’esperimento, ammesso funzioni, poterà alla creazione di particelle subatomiche, componenti essenziali per formare tutte le cose che ci stanno intorno e noi stessi.
Tra i primi a ipotizzare che si potesse ottenere la materia dalle particelle di luce, cioè i fotoni, ci furono i fisici statunitensi Gregory Breit e John Wheeler. Negli anni Trenta del Novecento scoprirono che due fotoni in alcune circostanze si possono combinare tra loro portando alla formazione di un elettrone e di un positrone (l’antiparticella dell’elettrone). Gli elettroni sono particelle subatomiche e, semplificando, possono essere considerati il “guscio” degli atomi.
Nel loro studio, Breit e Wheeler scrissero che comunque la loro teoria sarebbe stata molto difficile da dimostrare nella pratica. Scrissero che produrre l’interazione tra i due fotoni non era per nulla semplice e che provare a realizzarla in laboratorio, per lo meno con i mezzi dell’epoca, era una cosa senza speranza. Secondo molti, quella di Breit e Wheeler è tra le migliori teorie formulate per dimostrare la famosa equazione E=mc2 di Albert Einstein, che stabilisce l’equivalenza e il fattore con cui avviene la conversione tra energia e massa in un sistema (la “c” indica la costante della velocità della luce, la “m” la massa di un corpo ed “E” l’energia contenuta o emessa dallo stesso corpo).
Il problema di ottenere la materia dai fotoni nei decenni seguenti fu affrontato da diversi ricercatori. Nel 1997 lo Stanford Linear Accelerator Center in California ci andò molto vicino, ma per ottenere il risultato previsto dalla teoria di Breit e Wheeler i fisici dovettero introdurre nel sistema alcune particelle che già avevano una massa. La novità del Blackett Laboratory sta nel fatto che il nuovo processo prevede il solo utilizzo di fotoni: luce e basta, insomma.

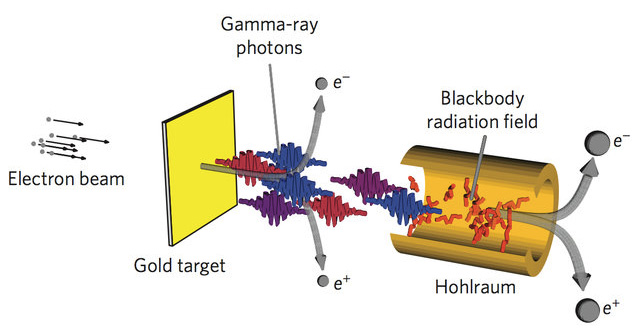
Nella ricerca pubblicata su Nature Photonics, Pike e colleghi spiegano come intendono raggiungere il loro obiettivo. In una prima fase si bombarda una placca d’oro con un fascio di elettroni per produrre un raggio di fotoni ad alta energia. Separatamente, un laser ad alta energia viene indirizzato verso una capsula cava d’oro, portando all’emissione di un raggio di luce molto intenso paragonabile a quella emessa dalle stelle. Infine, il primo fascio di fotoni viene indirizzato verso la capsula, facendo in modo che i fotoni collidano tra loro producendo gli elettroni. Il processo, scrivono i ricercatori, porta alla produzione di circa 100mila coppie di elettroni/positroni.
Oggi esistono diversi centri di ricerca in giro per il mondo che hanno le capacità e le strumentazioni necessarie per portare dalla teoria alla pratica il metodo proposto dai fisici del Blackett Laboratory. Nello studio non si specifica quale centro sarà utilizzato, ma diverse organizzazioni potrebbero essere interessate a condurre l’esperimento. Dal suo esito si potrebbero ottenere nuove informazioni per capire meglio i rapporti tra energia e materia, fondamentali per l’esistenza, di tutto.
Sin dai tempi dei filosofi greci l’uomo cerca di capire di cosa sia fatta la materia che lo circonda. Nella fisica moderna, uno dei metodi più fruttuosi per esplorare la struttura della materia alle scale più piccole è quello di “sparare”, con macchine dedicate chiamate acceleratori di particelle, particelle elementari elettricamente cariche, per esempio elettroni, contro campioni di materia. Lo scontro può avvenire attraverso lo scambio di un fotone virtuale, che permette, in un certo senso, di “vedere” l’interno della materia (vd. approfondimento "Luce virtuale"). Il primo successo di questa tecnica fu la scoperta del nucleo dell’atomo. Nel 1910 Hans Geiger e Ernest Marsden spararono particelle alfa, ovvero particelle cariche prodotte nei decadimenti radioattivi, contro una lamina d’oro. Grazie a questi urti, che oggi descriviamo come mediati da uno scambio di fotoni virtuali, Ernest Rutherford capì che doveva esserci un oggetto di dimensioni molto più piccole di quelle dell’atomo, ma che ne conteneva quasi tutta la massa: il nucleo.
 a.L'acceleratore Hera del laboratorio Desy di Amburgo: un anello con una circonferenza di 6,3 km capace di far collidere protoni con elettroni per esplorare la struttura dei protoni fino a scale di dimensioni di 10-15 mm (un milionesimo di miliardesimo di mm).
a.L'acceleratore Hera del laboratorio Desy di Amburgo: un anello con una circonferenza di 6,3 km capace di far collidere protoni con elettroni per esplorare la struttura dei protoni fino a scale di dimensioni di 10-15 mm (un milionesimo di miliardesimo di mm).Luce virtuale
L’avvento di acceleratori di particelle sempre più potenti, in cui fasci di elettroni venivano sparati contro bersagli fissi, ha permesso di distinguere dettagli sempre più piccoli all'interno della materia. Fino agli anni '50 si pensava, ad esempio, che il protone, uno dei componenti del nucleo di un atomo, fosse una particella "elementare" ovvero puntiforme. Usando un acceleratore di elettroni del laboratorio Slac in California, Robert Hofstadter trovò invece che il protone ha un'estensione spaziale misurabile, con un raggio di circa un decimillesimo di miliardesimo di centimetro (10-13 cm). L'acceleratore lineare che entrò in funzione allo Slac nel 1967 portò a una nuova svolta nel campo della fisica delle particelle: la scoperta di oggetti puntiformi all'interno del protone, i quark. Successivamente vari esperimenti, effettuati ai laboratori Cern di Ginevra e Fermilab vicino Chicago, hanno studiato la struttura interna del protone usando come sonde non solo elettroni, ma anche altre particelle come muoni e neutrini. Un salto quantitativo nella capacità di distinguere strutture sempre più piccole si è ottenuto negli anni '90 con Hera (Hadron Elektron Ring Anlage), dove fasci di elettroni ad alta energia venivano fatti scontrare con protoni a loro volta accelerati. L'acceleratore Hera è rimasto in funzione per circa 15 anni, dal 1992 al 2007, presso il laboratorio Desy di Amburgo (Germania). Il contributo dell'Infn, consistente nella fornitura di metà dei magneti superconduttori usati per il fascio dei protoni, è stato fondamentale per la realizzazione dell'acceleratore. L'Infn ha anche partecipato alla costruzione e al funzionamento dei due esperimenti (H1 e Zeus), posti nei punti di collisione elettrone-protone, e dei due esperimenti (Hermes e Herab), che hanno studiato le collisioni su bersagli fissi. I fisici italiani sono ancora impegnati nell'analisi dei dati raccolti da Hera, che hanno portato a una visione più completa del protone e a una verifica dettagliata della teoria delle interazioni forti, la cromodinamica quantistica o Qcd, dall'acronimo inglese quantum-chromo-dynamics (vd. approfondimento "Luce virtuale"). Ma i quark sono oggetti elementari od oggetti dotati a loro volta di una struttura? Le misure a Hera ci dicono che i quark sono puntiformi o meglio che il loro raggio deve essere più piccolo di un millesimo del raggio del protone. I quark up e down presenti nel protone (e nel neutrone, l'altro componente del nucleo di un atomo) e l'elettrone rimangono quindi, al momento, i più piccoli mattoni di cui è composta la materia ordinaria. Non è però stata ancora detta l'ultima parola nel campo delle collisioni elettrone-protone. Si sta già progettando infatti una nuova macchina, chiamata Lhec (Large Hadron-Electron Collider), che dovrebbe sparare fasci di elettroni contro protoni accelerati alle altissime energie dell'acceleratore Lhc del Cern a Ginevra. In questo modo si potrebbero studiare strutture dieci volte più piccole di quelle esplorate finora (vd. fig. b).
Fotoni contro fotoni
Massa infinita, massa zero o quale alla velocità della luce?
In altra parte del mio blog mi ero posto (e credo anche voi) la domanda: cos’ha di speciale la velocità della luce da non poter essere superata.
La velocità di propagazione di qualsiasi corpo dipende dal mezzo che attraversa.
Non sfugge a questa regola nemmeno la luce.
Non sfugge a questa regola nemmeno la luce.
La differenza sta nel fatto che la luce essendo contemporaneamente particella ed onda, la sua velocità nel propagarsi nello spazio dipende dal campo elettromagnetico che attraversa.
Precisamente
Dove co è la velocita della luce nel vuoto ed i termini al denominatore sono rispettivamente la permettività elettrica e la permettività magnetica nel vuoto.
Dimostrare la insuperabilità della velocità luce da questa formula è cosa impossibile. Bisogna accettarla e basta perché le permettività sono delle costanti universali.
Dimostrare la insuperabilità della velocità luce da questa formula è cosa impossibile. Bisogna accettarla e basta perché le permettività sono delle costanti universali.
Per dare risposta invece alla domanda: “cosa succede ad una massa quando è prossima alla velocità della luce” ho fatto ricorso alla famosa legge di Einstein, dove la massa è legata alla sua energia e alla velocità della luce.
Giusto o sbagliato sono andato avanti lo stesso per vedere cosa succedeva.
Giusto o sbagliato sono andato avanti lo stesso per vedere cosa succedeva.
E’ noto a tutti che:
E = m c2
(formula 1)
“E” è l’energia emessa o contenuta da una massa, “m” è la massa corrispondente, “c” la velocità della luce.
In realtà gli articoli originali di Einstein trattavano “m” come “massa relativistica“. Questa è stata relazionata da Hendrik Lorenz alla “massa a riposo” m0 (cioè la massa dell’oggetto nel sistema di riferimento in cui è in quiete) tramite un fattore (fattore di Lorentz) che ha preso il suo nome.
nel modo seguente per tener conto delle velocità prossime a quella della luce:
(formula 2)
Dove “v” è la velocità del corpo.
Ora, per comodità di scrittura, considero m=massa a riposo.
La formula di Einstein così corretta diventa:
La formula di Einstein così corretta diventa:
(formula 3)
Quindi:
In altre parole, per accelerare una massa a velocità superiori alla luce, serve una quantità infinita di energia.
Bene, fin qui siamo tutti d’accordo. Credo di si.
Ora la domanda è quale valore raggiunge la massa a velocità della luce.
Ora la domanda è quale valore raggiunge la massa a velocità della luce.
La risposta la sappiano tutti. L’abbiamo letta più volte e dobbiamo accettarla perchè lo dicono quelli più bravi di noi.
Nonostante questo voglio mettervi una pulce nell’orecchio.
Di cosa si tratta? Di un semplice ragionamento che per dargli un minimo di credibilità ho cercato conforto in chi ne sa più di me presentando il mio ragionamento. Persone che fanno informazione scientifica e scrivono cose di astrofisica.
Non ho avuto spiegazioni, solo concettualità a me già note con tono accademico quasi a volermi dare lezioni. Ho capito, tutti professori, ma ragionamenti zero. Allora proseguo da solo.
Nonostante questo voglio mettervi una pulce nell’orecchio.
Di cosa si tratta? Di un semplice ragionamento che per dargli un minimo di credibilità ho cercato conforto in chi ne sa più di me presentando il mio ragionamento. Persone che fanno informazione scientifica e scrivono cose di astrofisica.
Non ho avuto spiegazioni, solo concettualità a me già note con tono accademico quasi a volermi dare lezioni. Ho capito, tutti professori, ma ragionamenti zero. Allora proseguo da solo.
Vediamo di cosa si tratta.
La prima cosa che viene in mente ad uno studente liceale è risolvere la stessa equazione di Einstein (formula 3) rispetto ad “m”, dove massa ed energia sono legate “indissolubilmente insieme”. I fotoni, ricordiamo, trasportano energia.
La prima cosa che viene in mente ad uno studente liceale è risolvere la stessa equazione di Einstein (formula 3) rispetto ad “m”, dove massa ed energia sono legate “indissolubilmente insieme”. I fotoni, ricordiamo, trasportano energia.
Ma ecco che succedono cose strane o per meglio dire cose controverse, non accettate dalla scienza.
Spiego.
Spiego.
Sappiamo che il fattore di Lorenz va all’infinito per v=c, e il suo inverso (ovvero la radice) va a zero.
Si trova facilmente che per v=c la equazione 3) di Einstein, in funzione di m, da questo risultato:
m c2 = E *0
quindi
m = 0 (essendo c2 una costante)
ovvero alla velocità della luce la massa a riposo diventa zero.
Si trova facilmente che per v=c la equazione 3) di Einstein, in funzione di m, da questo risultato:
m c2 = E *0
quindi
m = 0 (essendo c2 una costante)
ovvero alla velocità della luce la massa a riposo diventa zero.
Orrore!
Eppure qualcosa vuol dire. Tutte le teorie portano, infatti, a dire che alla velocità della luce la massa a riposo tende a infinito. Eppure la soluzione della equazione è esatta.
D’altra parte i fotoni (sono anche perticelle, ricordiamocelo) che viaggiano alla velocità della luce, guarda caso hanno massa nulla e non infinita.
I fisici dicono che questo succede proprio perchè i fotoni hanno massa a riposo nulla, ovvero zero.
Eppure qualcosa vuol dire. Tutte le teorie portano, infatti, a dire che alla velocità della luce la massa a riposo tende a infinito. Eppure la soluzione della equazione è esatta.
D’altra parte i fotoni (sono anche perticelle, ricordiamocelo) che viaggiano alla velocità della luce, guarda caso hanno massa nulla e non infinita.
I fisici dicono che questo succede proprio perchè i fotoni hanno massa a riposo nulla, ovvero zero.
Bene, allora, dato che i fotoni hanno massa nulla, ma sono anche particelle elementari, allora provate a mettere il valore zero di ‘m’ nella formula 3). Cosa succede?
Un casino.
A velocità della luce il numeratore è zero, il denominatore va a zero, ovvero l’equazione (E=c20/0) assume un valore indeterminato.
Un casino.
A velocità della luce il numeratore è zero, il denominatore va a zero, ovvero l’equazione (E=c20/0) assume un valore indeterminato.
Stessa cosa nella formula 2).
Sappiamo che non è così. Tuttavia i fisici dicono che in questo caso, ovvero per masse nulle, queste formule non valgono in quanto i fotoni seguono le equazioni d’onda elettromagnetica, anche se la comunità scientifica non è concorde su questo fatto. Insomma anche gli autorevoli scienziati non sono tutti daccordo.
E la confusione aumenta.
Sappiamo che non è così. Tuttavia i fisici dicono che in questo caso, ovvero per masse nulle, queste formule non valgono in quanto i fotoni seguono le equazioni d’onda elettromagnetica, anche se la comunità scientifica non è concorde su questo fatto. Insomma anche gli autorevoli scienziati non sono tutti daccordo.
E la confusione aumenta.
Ma c’è dell’altro.
Nessuna massa può diventare infinita per il semplice fatto che nell’ipotetico caso “v” dovesse “appena” superare la velocità della luce, v>c, la massa diventa “immaginaria” a causa della radice nel fattore di Lorenz che diventa negativa.
Infatti essendo β >1 si ha una radice di un numero negativo con massa relativistica immaginaria.
con massa relativistica immaginaria.
Nessuna massa può diventare infinita per il semplice fatto che nell’ipotetico caso “v” dovesse “appena” superare la velocità della luce, v>c, la massa diventa “immaginaria” a causa della radice nel fattore di Lorenz che diventa negativa.
Infatti essendo β >1 si ha una radice di un numero negativo
 con massa relativistica immaginaria.
con massa relativistica immaginaria.
Detta in altre parole, nel momento in cui la massa raggiunge la velocità delle luce diventa improvvisamente immaginaria facendo comparire le famose particelle “virtuali” chiamate tachioni, di massa immaginaria per l’appunto, che viaggerebbero indisturbate nell’universo a massa immaginaria ‘non infinita’ ad energia negativa.
Questa è una conseguenza della relatività ristretta in quanto il tachione, in teoria, per v>c ha una massa che elevata al quadrato “passa di colpo” a valori negativi, insomma la massa assume di colpo valori negativi dopo aver avuto valore infinito un istante prima.
Gli scienziati bocciano questa ipotesi; una semplice considerazione matematica – dicono – nessuna massa infatti può superare la velocità della luce. Nessun elettrone può avere energia negativa.
Gli scienziati bocciano questa ipotesi; una semplice considerazione matematica – dicono – nessuna massa infatti può superare la velocità della luce. Nessun elettrone può avere energia negativa.
Questo non è vero. Non è più vero per un elettrone virtuale, che può avere qualsiasi valore di energia. Un elettrone libero può emettere un fotone virtuale divenendo esso stesso virtuale per poi ritornare reale. Nella fase di transizione l’elettrone e il fotone virtuali hanno una gamma di energie possibili. Per esempio, il fotone virtuale può essere molto energetico, mentre l’elettrone virtuale può avere energia negativa. (Diagrammi di Feynman)
La confusione aumenta.
La confusione aumenta.
Allora mi domando cosa c’è di sbagliato nel ricavare il valore della massa dalla legge di Eintein.
Qualcosa mi sfugge. Mi arrendo.
Qualcosa mi sfugge. Mi arrendo.
In realtà qualcuno mi è venuto in soccorso.
Un fisico teorico (ex amico) che dovrebbe avere le conoscenze giuste si è avventurato proponendomi improbabili calcoli sulla stessa formula 3) di Einstein con l’aggravante di commettere macroscopici errori di calcolo inciampando malamente sulle regole delle frazioni pur di dimostrare il contrario, raccogliendo solo una gran figuraccia.
Un fisico teorico (ex amico) che dovrebbe avere le conoscenze giuste si è avventurato proponendomi improbabili calcoli sulla stessa formula 3) di Einstein con l’aggravante di commettere macroscopici errori di calcolo inciampando malamente sulle regole delle frazioni pur di dimostrare il contrario, raccogliendo solo una gran figuraccia.
Se a questo punto vi state domandando come stanno le cose, ecco che interviene un altro amico di cui non posso dubitare.
Umberto Genovese che conduce il blog “il Poliedrico” mi scrive.
Umberto Genovese che conduce il blog “il Poliedrico” mi scrive.
E= m*c^2 vale solo ed esclusivamente se m è assunta come massa a riposo (che indicherò con m_o). A velocità al di sotto del 10% di c (c=299792458 m/s arrotondato a 3E+8 m/s ed è costante nel vuoto per i fotoni che sono privi di massa) l’invarianza di Lorentz in genere non si applica data l’esiguità del suo apporto al computo totale della massa.
Lascia perdere per un attimo l’equazione di Einstein per questo ragionamento e concentrati sul principio dell’invarianza di Lorentz. che sappiamo essere m = m_o/(v^2/c^2)^1/2.
Se prendiamo un oggetto con una massa a riposo molto piccola (m_o = 0,5 Mev per l’elettrone) quando viene accelerato vicino a c (99,9% di questa), tipico negli acceleratori come l’LHC, si avrà una massa che arriva a 11 Mev, mentre al 99,99% di c, un incremento quindi di solo lo 0,01%, diventa di 35 Mev. Ogni piccolo incremento, per quanto piccolo, porterà ad una crescita esponenziale della massa dell’elettrone.
Quindi come vedi, la massa ad approssimarsi di c (che è ripeto, una costante nel vuoto) tende a crescere esponenzialmente fino a diventare infinita. Solo i fotoni che non hanno massa raggiungono tali velocità, tutte le altre particelle dotate di massa, per quanto piccola essa sia (vedi i neutrini) non la possono eguagliare.
I neutrini appunto mi danno lo spunto per farti un esempio: la loro strana capacità di oscillare tra i loro sapori con le differenti masse conseguenti, permette loro di variare la velocità nel loro percorso. per questo ne osserviamo i diversi sapori: diverse masse, diverse velocità.
Lascia perdere per un attimo l’equazione di Einstein per questo ragionamento e concentrati sul principio dell’invarianza di Lorentz. che sappiamo essere m = m_o/(v^2/c^2)^1/2.
Se prendiamo un oggetto con una massa a riposo molto piccola (m_o = 0,5 Mev per l’elettrone) quando viene accelerato vicino a c (99,9% di questa), tipico negli acceleratori come l’LHC, si avrà una massa che arriva a 11 Mev, mentre al 99,99% di c, un incremento quindi di solo lo 0,01%, diventa di 35 Mev. Ogni piccolo incremento, per quanto piccolo, porterà ad una crescita esponenziale della massa dell’elettrone.
Quindi come vedi, la massa ad approssimarsi di c (che è ripeto, una costante nel vuoto) tende a crescere esponenzialmente fino a diventare infinita. Solo i fotoni che non hanno massa raggiungono tali velocità, tutte le altre particelle dotate di massa, per quanto piccola essa sia (vedi i neutrini) non la possono eguagliare.
I neutrini appunto mi danno lo spunto per farti un esempio: la loro strana capacità di oscillare tra i loro sapori con le differenti masse conseguenti, permette loro di variare la velocità nel loro percorso. per questo ne osserviamo i diversi sapori: diverse masse, diverse velocità.
Tutto giusto. Ma queste cose le sapevamo già e non trovo traccia del mio errore.
Anche qui faccio qualche osservazione.
I “neutrini” (sparati da una supernova collassata) “hanno” massa per quanto piccola.
Per quanto abbiano “sapori” diversi si pensava che essi viaggiassero a velocità superluminale vagando nello spazio. Questo significa che hanno velocità prossima a quella della luce, ma non hanno massa “quasi” prossima ad un valore infinito come previsto dalla teoria. Infatti la sua massa a velocità prossime a quella della luce è circa 0,05 eV/c2.
Nessun neutrino a massa quasi infinta è stato osservato in laboratorio e nello spazio.
I “neutrini” (sparati da una supernova collassata) “hanno” massa per quanto piccola.
Per quanto abbiano “sapori” diversi si pensava che essi viaggiassero a velocità superluminale vagando nello spazio. Questo significa che hanno velocità prossima a quella della luce, ma non hanno massa “quasi” prossima ad un valore infinito come previsto dalla teoria. Infatti la sua massa a velocità prossime a quella della luce è circa 0,05 eV/c2.
Nessun neutrino a massa quasi infinta è stato osservato in laboratorio e nello spazio.
Gli stessi “muoni” che dopo gli eletroni sono le particelle più leggere, hanno velocità quasi uguale a quella della luce (il 99,92% di quella della luce, cioè v ≈ c), eppure non hanno massa quasi infinita.
Dove sta allora l’inghippo?
Secondo l’amico Umberto, (ma non solo), non bisogna scomodare l’equazione di Einstein, basta ragionare esclusivamente sul “fattore di Lorenz” che legato alla massa inerziale è proprio la famosa massa relativistica di Einstein.
Secondo l’amico Umberto, (ma non solo), non bisogna scomodare l’equazione di Einstein, basta ragionare esclusivamente sul “fattore di Lorenz” che legato alla massa inerziale è proprio la famosa massa relativistica di Einstein.
Da questa formuletta (2) infatti si ricava con un solo passaggio che per v=c la massa va all’infinito.
Tutto qui. Punto.
Tutto qui. Punto.
Facile no?
Troppo facile – penso – A questo c’ero arrivato anch’io, perchè in quella miracolosa formuletta la massa non ha alcun legame con la “sua” energia come deve essere. Una velocità mossa dal nulla. Un artifcio insomma che sembra fatto apposta per far tornare i conti. Quali conti?
Dove sta allora l’inghippo?
Troppo facile – penso – A questo c’ero arrivato anch’io, perchè in quella miracolosa formuletta la massa non ha alcun legame con la “sua” energia come deve essere. Una velocità mossa dal nulla. Un artifcio insomma che sembra fatto apposta per far tornare i conti. Quali conti?
Dove sta allora l’inghippo?
L’inghippo sta nel fatto che il fattore di Lorenz è semplicemnete una formuletta, scollegata dalla energia, secondo la quale una massa va all’infinito quando la sua velocità è al 99, 99999999 % ……. decimale ripetuto all’infinito.
Insomma, secondo il fattore di Lorenz, si corre il rischio che un giorno, quando riusciremo a fornire abbastanza energia ad un elettrone o un protone da farlo viaggiare in un acceleratore nucleare come l’LHC a velocità molto vicina quella della luce, questa massa potrà raggiungere la massa prossima a quella di una … galassia e forse oltre.
Insomma, secondo il fattore di Lorenz, si corre il rischio che un giorno, quando riusciremo a fornire abbastanza energia ad un elettrone o un protone da farlo viaggiare in un acceleratore nucleare come l’LHC a velocità molto vicina quella della luce, questa massa potrà raggiungere la massa prossima a quella di una … galassia e forse oltre.
Massa relativista, un concetto confuso.
A mio avviso, che ovviamente conta per quello che conta e mi scuso con i fisici teorici puri, la formula di Lorenz usata per spiegare l’aumento di massa con la velocità è confusa come è confusa la dimostrazione dell’aumento della massa. Almeno nel merito, perché la massa nella realtà non aumenta mai con l’aumento di energia, né tantomeno con la velocità, la massa invece ha la particolare capacità di caricarsi di energia supplementare proprio con la velocità. La formuletta di Lorenza infatti, come ho detto più volte, non lega la massa alla energia che conferisce l’aumento della velocità.
Faccio un esempio per capire meglio.
A mio avviso, che ovviamente conta per quello che conta e mi scuso con i fisici teorici puri, la formula di Lorenz usata per spiegare l’aumento di massa con la velocità è confusa come è confusa la dimostrazione dell’aumento della massa. Almeno nel merito, perché la massa nella realtà non aumenta mai con l’aumento di energia, né tantomeno con la velocità, la massa invece ha la particolare capacità di caricarsi di energia supplementare proprio con la velocità. La formuletta di Lorenza infatti, come ho detto più volte, non lega la massa alla energia che conferisce l’aumento della velocità.
Faccio un esempio per capire meglio.
Se noi prendiamo tre proiettili da 20 grammi, il primo è fermo, il secondo lo lanciamo a 1km/s con una normale pistola il terzo lo lanciamo ad una velocità prossima a quella della luce, con questo esperimento noi abbiamo sempre un proiettile di 20 grammi di massa ma con tre comportamenti diversi.
Il primo proiettile: la massa è a riposo ed ha solo una inerzia di 20 grammi dato che l’esperimento lo eseguiamo sulla terra.
Il secondo proiettile ha una maggiore energia cinetica che rende il proiettile più perforante e pericoloso. Perché? Perché oltre al suo peso si aggiunge l’energia cinetica per arrivare ad 1km/s, perciò il proiettile con i suoi 20 grammi di massa esercita un’inerzia sempre proporzionale alla sua velocità nell’avanzare ed è questa inerzia a creare un ulteriore aumento di energia cinetica al suo interno proporzionale alla sua velocità ed alla sua massa.
Terzo proiettile. Per spiegare cosa succede al proiettile quando raggiunge velocità prossime alla luce viene introdotto il fattore di Lorenz che introduce il concetto di massa relativista (mƴ) che ha una dimensione di una energia (mƴ=m’=E/c2 ) a meno di un fattore della velocità della luce al quadrato, impropriamente preso come unità di misura della massa relativista.
In pratica per cercare di portare il proiettile ad una velocità prossima a quella della luce, noi dobbiamo utilizzare tantissima energia (considerate che anche LCH l’acceleratore di particelle più grande al mondo non è in grado di mandare un proiettile di 20 grammi alla velocità della luce), molta di questa energia viene incamerata proprio nella sua massa sotto forma di energia.
Non è la massa ad aumentare è proprio la sua inerzia a caricarsi, che trattenendo l’avanzamento del proiettile accumula energia cinetica al suo interno, come un volano.
Non è la massa ad aumentare è proprio la sua inerzia a caricarsi, che trattenendo l’avanzamento del proiettile accumula energia cinetica al suo interno, come un volano.
Perciò è corretto dire che non è un aumento di massa ma è un aumento d’inerzia della massa che accumula l’energia cinetica nella massa. E’ questa energia che tende all’infinito alla velocità della luce.
Ma voglio andare oltre.
Il proiettile è composto di molecole ed atomi che sono legati tra loro da forze molecolari ed atomiche. Per una massa infinita la energia fornita al proiettile dovrebbe dare forza infinita alla forza che trattiene i quark e elettroni (forza forte, debole, elettromagnetica) per non far “esplodere” il proiettile. In pratica si dovrebbe riscrivere il modello standard a velocità superluminari.
Il proiettile è composto di molecole ed atomi che sono legati tra loro da forze molecolari ed atomiche. Per una massa infinita la energia fornita al proiettile dovrebbe dare forza infinita alla forza che trattiene i quark e elettroni (forza forte, debole, elettromagnetica) per non far “esplodere” il proiettile. In pratica si dovrebbe riscrivere il modello standard a velocità superluminari.
A questo punto faccio un’altra osservazione, perchè sono testardo.
La trasformata di Lorenz è una equazione che lega il primo termine al secondo termine tramite il segno uguale.
La trasformata di Lorenz è una equazione che lega il primo termine al secondo termine tramite il segno uguale.
Bene, provate ora a mettere il valore zero alla massa a riposo per vedere cosa succede per v=c
m=0/0.
La massa relativistica è indeterminata. Altro casino.
E siamo punto da capo.
m=0/0.
La massa relativistica è indeterminata. Altro casino.
E siamo punto da capo.
Il paradosso della energia e massa infinita per v=c
Se veramente energia e massa tendono contemporaneamente a infinito per v=c, cosa succede alla velocità della luce? Dalla formuletta di Einstein si ricava:
E=mƴc2
dove mƴ=m’= massa relativista.
Quindi:
c2=E/m’
Dal momento che per v=c E=m’=infinito
Se veramente energia e massa tendono contemporaneamente a infinito per v=c, cosa succede alla velocità della luce? Dalla formuletta di Einstein si ricava:
E=mƴc2
dove mƴ=m’= massa relativista.
Quindi:
c2=E/m’
Dal momento che per v=c E=m’=infinito
c2=infinito/infinito=indeterminata
Non c’è bisogno di spiegazioni. Un paradosso.
Scoraggiato, allora, mi rifugio su Wikipedia. Ma leggendo qua e là scopro che poi la confusione non ce l’ho solo io.
Infatti leggo:
“Il fattore di Lorenz è considerato ambiguo dai molti fisici”
Ma va? – rifletto – proprio il fattore da cui si basa la certezza che la massa va all’infinito.
“Il fattore di Lorenz è considerato ambiguo dai molti fisici”
Ma va? – rifletto – proprio il fattore da cui si basa la certezza che la massa va all’infinito.
Ancora.
“È tuttora in corso una discussione vertente sulla possibilità di definire la massa relativistica come la massa.”
Ma come? – penso – non era tutto risolto?
Un altro bel casino perchè tutto verrebbe messo in discussione.
“È tuttora in corso una discussione vertente sulla possibilità di definire la massa relativistica come la massa.”
Ma come? – penso – non era tutto risolto?
Un altro bel casino perchè tutto verrebbe messo in discussione.
Ed ancora.
“L’utilizzo della massa relativistica è attualmente deprecato in ambito scientifico (e didattico) per vari motivi, quale ad esempio il fatto che essa, a meno di un fattore c2, è un altro nome per indicare l’energia di una particella (massa relativistica ed energia sono direttamente proporzionali)”.
“L’utilizzo della massa relativistica è attualmente deprecato in ambito scientifico (e didattico) per vari motivi, quale ad esempio il fatto che essa, a meno di un fattore c2, è un altro nome per indicare l’energia di una particella (massa relativistica ed energia sono direttamente proporzionali)”.
In un sistema isolato la massa relativistica si conserva per il principio della conservazione della materia infatti:

cioè la massa relativistica di un sistema isolato si conserva, come è ovvio notando che la massa relativistica è direttamente proporzionale all’energia.
Vacca boia, vuoi vedere che ho ragione?
Massa e energia vanno, infatti, considerate direttamente proporzionali.
Vuoi vedere che è un riferimento esplicito al mio paradosso che lega la massa alla energia?
c2 = E/m = infinito / infinito
Massa e energia vanno, infatti, considerate direttamente proporzionali.
Vuoi vedere che è un riferimento esplicito al mio paradosso che lega la massa alla energia?
c2 = E/m = infinito / infinito
Ma non è finita.
Infatti, in realtà è più propriamente definita massa relativistica la sua quantità di moto:
p = mv
La energia della massa in movimento è così espressa:
E = pc + m0 c2
dove m0 è la massa a riposo.
Che rappresenta l’energia di una massa in movimento non infinita per v=c dal momento che scompare il fattore di Lorenz.
Infatti, in realtà è più propriamente definita massa relativistica la sua quantità di moto:
p = mv
La energia della massa in movimento è così espressa:
E = pc + m0 c2
dove m0 è la massa a riposo.
Che rappresenta l’energia di una massa in movimento non infinita per v=c dal momento che scompare il fattore di Lorenz.
Allora:
E = E1 + E2
Si ricava:
mv = E/c – m0c
Per v=c, è la quantità di moto che aumenta. Se vogliamo calcolare la massa (m) in movimento si ricava
m=E/c2-m0
ovvero una massa non infinita, nè nulla per v=c avendo E un valore finito.
E = E1 + E2
Si ricava:
mv = E/c – m0c
Per v=c, è la quantità di moto che aumenta. Se vogliamo calcolare la massa (m) in movimento si ricava
m=E/c2-m0
ovvero una massa non infinita, nè nulla per v=c avendo E un valore finito.
Ora per v=0
0 = E/c – m0 c
Che ci riporta alla energia di una massa a riposo.
E0 = m0 c2
E i conti tornano.
0 = E/c – m0 c
Che ci riporta alla energia di una massa a riposo.
E0 = m0 c2
E i conti tornano.
La massa (m0) del protone deriva dalla sua energia espressa in unità corrispondenti alla velocità della luce al quadrato (c2). Anche la massa degli stessi quark non dipende solo dal movimento ma anche dalla energia di legame con i gluoni.
Conclusione.
Se la massa relativistica è deprecata in ambito scientifico e didattico, non c’è certezza sul reale signficato di massa relativistica e di conseguenza sul valore della massa a velocità prossime alla luce.
Se la massa relativistica è deprecata in ambito scientifico e didattico, non c’è certezza sul reale signficato di massa relativistica e di conseguenza sul valore della massa a velocità prossime alla luce.
In definitiva la massa perde il suo significato classico assumendo il valore di una energia rapportata al quadrato della velocità della luce.
Il valore della massa a velocità della luce non può essere calcolato dal fattore di Lorenz dal momento che energia e massa devono essere collegate indissolubilmente assieme come è chiaramente evidenziato dalla formula di Einstein e confermato dalle masse relativistiche delle particelle subatomiche (E=mc2). Quello che si osserva negli acceleratori delle particelle, e a prova dei fisici, non è un aumento della massa relativistica ma qualcos’altro, incrementato di un fattore delle velocità della luce al quadrato.
La massa relativistica non può più essere chiamata massa.
E’ possibile osservare in Natura la trasformazione di energia in materia? Se no, sarebbe possibile, in teoria, a temperature molto basse prossime allo 0 assoluto osservare la trasformazione di energia in particelle elementari di materia? Grazie
La risposta alla prima domanda cambia a seconda di cosa si intenda per trasformazione energia-materia.
Se ci riferiamo alla semplice scomparsa di energia in una qualsiasi forma (calore, energia cinetica, energia di campo) in una data regione di spazio con conseguente aumento di massa dei corpi presenti in quella stessa regione di spazio, allora questo avviene in tutte le reazioni chimiche endotermiche, cioè quelle che possono avvenire solo assorbendo energia dall’ambiente esterno. In tutti questi casi si può osservare (naturalmente con misure molto precise) che la massa dei prodotti di reazione è maggiore della massa dei reagenti. La massa in più è data dall’energia assorbita che è stata trasformata in massa. Un altro esempio è la ionizzazione di un atomo o di una molecola, che può avvenire solo a seguito dell’assorbimento di un fotone che faccia saltare l’elettrone fuori dagli stati legati. In seguito a questo salto la massa dello ione+elettrone è maggiore di quella dell’atomo neutro (per questo l’atomo non si ionizza spontaneamente) e la massa in più è esattamente equivalente all’energia assorbita secondo la famosa equazione
E=mc2
Se invece si intende la scomparsa di energia cinetica o di campo (in tal caso è più preciso parlare di scomparsa di bosoni vettori, cioè di quelle particelle che, come i fotoni, trasportano le interazioni e che quindi rappresentano la parte energetica di un sistema) in cambio della comparsa di coppie di fermioni (le particelle come elettroni, protoni e neutroni che costituiscono ciò che normalmente chiamiamo materia) e antifermioni (la creazione di materia può avvenire solo creando contemporanemente una quantità uguale di antimateria) allora la risposta è negativa.
Per creare anche il fermione più leggero, l’elettrone (trascuro il neutrino che interagendo solo mediante la forza nucleare debole di fatto è coinvolto in fenomeni lontanissimi dall’esperienza comune) è necessaria una quantità di energia molto grande concentrata in un solo fotone (se in presenza di campi di forze esterni), in una singola coppia di fotoni o in una singola coppia di particelle che si urtano (se ci si trova nel vuoto), il che vuol dire radiazioni a frequenza molto più elevata di quelle che si osservano sulla Terra.
Naturalmente le cose cambiano se si parla di ciò che accade all’interno delle stelle, in particolare nelle supernovae. In queste stelle le grandi esplosioni forniscono energia sufficiente a trasformazioni di ogni tipo. Tanto è vero che è proprio all’interno di queste esplosioni che avviene la creazione degli elementi più pesanti del ferro i cui nuclei in generale pesano di più dei loro singoli elementi che li compongono pesati separatamente. Tuttavia questa creazione di materia rientra comunque nel primo tipo (anche se le reazioni coinvolte sono nucleari invece che chimiche) in quanto le coppie particella-antiparticelle tendono a riannichilarsi poco dopo la loro creazione (dato che hanno carica elettrica opposta) restituendo l’energia sotto forma di radiazione.
Da ciò che ho detto risulta evidente che quello che viene ipotizzato nella seconda domanda è sbagliato. La creazione di materia dall’energia richiede alte velocità e quindi alte temperature. A basse temperature certamente non può avvenire. Quando un sistema si raffredda, ciò avviene perchè viene sottratta energia, e ci si avvicina allo zero assoluto quando la sua energia interna si avvicina al suo minimo assoluto a seguito di questa sottrazione.
Da:
https://www.vialattea.net/content/2871/
http://www.borborigmi.org/2008/10/28/massa-velocita-energia-la-formula-piu-famosa-del-mondo-e-il-teorema-di-pitagora/
https://www.matematicamente.it/appunti/fisica-per-le-superiori/la-relativita/equivalenza-massa-energia/
https://silvanodonofrio.wordpress.com/2014/07/19/massa-infinita-o-massa-zero-alla-velocita-della-luce/
https://www.asimmetrie.it/illuminando-la-materia
https://www.ilpost.it/2014/05/19/esperimento-materia-luce-fotoni-elettroni/



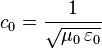

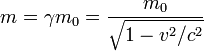
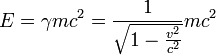
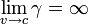
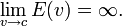



Commenti
Posta un commento